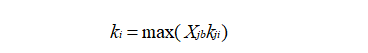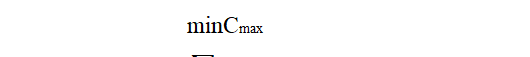Dear AMPL customer servicer:
Hello!I have some questions about AMPL I would like to ask you.My research problem is the problem of assembly shop scheduling.But I had trouble building models with AMPL.Here are my questions:
The first one,as shown in Figure 1, I want to ask for the maximum value in parentheses, whether there are any functions in AMPL that can directly find the maximum value, or if it needs to be linearized like Figure 2, and whether my linearization is correct …
Figure 1:
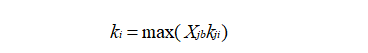
Figure 2:

Secondly, as shown in Figure 3, how these two constraints should be written in AMPL, should they also be linearized?
Figure 3:

The lastly, as shown in Figure 4, my problem is the assembly shop scheduling problem, the final target value is to minimize the maximum completion time, this is calculated in the constraint, how to write this goal in AMPL?
Figure 4:
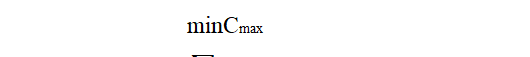
Looking forward to your response!
Thank you!
(1) For any two expressions x and y, you can write max(x,y) in AMPL. I suggest that you first formulate your constraint using this max function. Then to get more help, send your constraint and also the definitions of all sets, parameters, and variables used in the constraint. Also say what solvers you are considering, if you know. With that information, I can suggest whether you need to linearize the max function, and if so, how to do it.
(2) You could certainly write an AMPL expression that corresponds to this. For example, it might be:
Qpick[n] >= tpick[b] * (1+alpha)^(n-k[n]) + M * (Z[b,n]-1)
Again, however, you need to give definitions of all the sets, parameters, and variables that are needed for this constraint, before you can write the whole “subject to” statement in AMPL. Also, it is necessary to know which symbols are variables and which are parameters (data), in order to say whether the constraint can be linearized.
(3) If your model has a variable Cmax, and if it has some constraints that determine the value of Cmax, then you can define the objective function with a statement like this:
minimize MaxCompletionTime: Cmax;